How We Harness Industrial Generative AI for Optimization
How We Harness Industrial Generative AI for Optimization
In recently published research, we used a proprietary generative AI technique called GEO (Generator-Enhanced Optimization) to help BMW optimize the way they schedule their manufacturing plants. GEO not only generated new solutions to the problem, but in 71% of problem configurations, these solutions tied or improved upon solutions generated by the best traditional optimization algorithms.
What is GEO? How does it work, what sets it apart, and what problems is it best suited for? More importantly, is it the future of solving industrial optimization problems? If you’re wondering, this is the blog post for you.
For a global manufacturer like BMW, there were 244 million ways to solve this problem. Each step in the manufacturing process — body, paint, and assembly — has multiple shops, each with its own set of possible shift schedules and production rates. What’s more, the storage lots between each production shop also need to be kept stocked consistently to prevent shortages or overflows.
It’s a tricky problem with a lot of constraints. But by minimizing idle time at each step, BMW could stand to save millions in operational costs over the course of a year. With so much at stake, BMW worked with us to make their manufacturing process more efficient by harnessing generative AI.
For a global manufacturer like BMW, there were 244 million ways to solve this problem.
Much like how ChatGPT is trained on gigabytes of text on the internet, we trained our own generative model on the best solutions generated by the best conventional optimization algorithms — simulated annealing, genetic algorithms, parallel tempering, etc. The generative model then generated new shift schedule configurations. We found that GEO created solutions that tied or outperformed the solutions it was trained on 71% of the time.
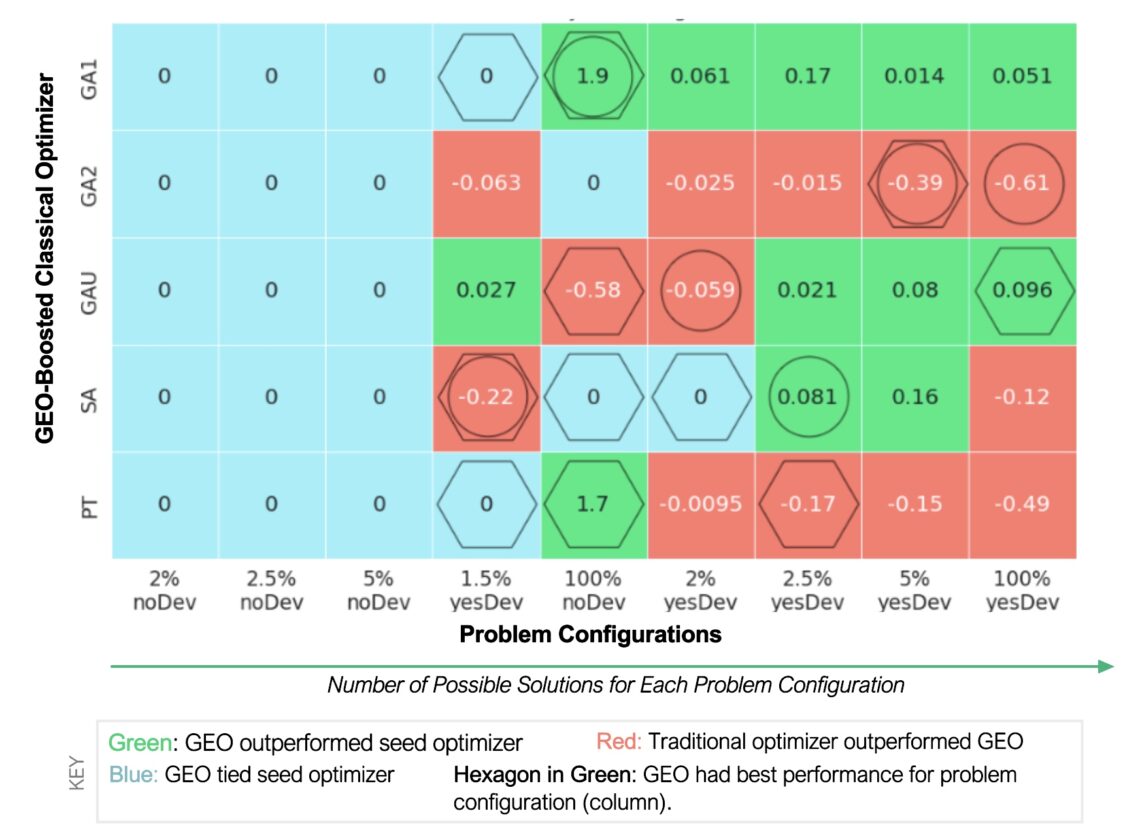
In particular, GEO provided the best solutions out of them all when the problem was configured to have the highest number of potential solutions. For example, by deviating the production rates between the shops instead of keeping them consistent, there would be many more possible solutions. For more complex industrial problems with an even bigger solution space, GEO could provide a major advantage.
For more complex industrial problems with an even bigger solution space, GEO could provide a major advantage.
Many companies already use conventional algorithms to optimize their operations and have a wealth of existing optimization solutions generated by these algorithms. With GEO, a generative model is trained on these existing solutions. If a company is starting from scratch and doesn’t already have an optimization algorithm in place, we can create sample data for the variables in question to train the model, even if this sample data would not result in an optimal solution at first.
From there, the generative model “learns” what makes a good solution. In other words, it learns the distribution of low-cost solutions based on the data provided. The model then generates new solutions that fall within this distribution. The best solutions, both those created by the generative model and those in the original training dataset, are used to train the model again and the cycle repeats, with the solutions getting better and better with more iterations.
This process works with any generative model. However, our research has shown that it works better with quantum generative models
This process works with any generative model. However, our research has shown that it works better with quantum generative models, or so-called “quantum-inspired generative models”, i.e., models based on quantum methods but running on classical hardware — as was the case in our work with BMW. This is because quantum models can improve upon classical models in terms of expressivity and generalization.
In generative modeling, expressivity refers to the range of possible probability distributions that can be represented, while generalization refers to the ability of a generative model to generate novel, high-quality samples, rather than simply repeating the training data. In the context of optimization, this means that quantum models can generate new solutions that were previously unconsidered, with potentially lower cost functions (the variable to be minimized) than previous solutions.
Whether you use a quantum generative model or a classical generative model, GEO comes with several advantages over conventional optimization algorithms.
Conventional optimization algorithms have become very effective at finding solutions to complex optimization problems across industries. GEO does not compete with these algorithms — it enhances them (of course, GEO can also work as a standalone solver). This de-risks the implementation of GEO, since if it turns out GEO doesn’t generate better solutions, you still have the conventional optimization algorithm.
GEO is flexible enough to be used for any optimization problem. As long as there is a dataset of solutions that can be used to train the generative model (and even if there isn’t, we can make one to initialize the process), GEO can be used to enhance the existing solutions.
For example, in addition to the work with BMW, we’ve also demonstrated how GEO can be used for optimizing financial portfolios. In that case, we were able to generate new portfolios with lower risk for the same level of return compared to the portfolios the model was trained on. In fact, GEO tied or outperformed the best-in-class portfolio optimization algorithms — fine-tuned over decades — 65% of the time (depending on the algorithm and the performance indicator used).
One caveat though is that just because GEO could work for any optimization problem, that doesn’t mean it should be used. In particular, GEO is not ideal for use cases where you want a solution within seconds, such as in high-speed trading. This isn’t because GEO wouldn’t perform well in these tasks per se, but because of the overhead time required to train a generative model. On the other hand, GEO does work exceptionally well for problems where the cost function is costly or time-consuming to evaluate, as in these scenarios this overhead becomes negligible.
In optimization, the cost function is the value that you want to minimize. GEO works with any cost function, no matter how difficult it is to compute. In fact, GEO provides a greater advantage for problems where cost function evaluation is time-consuming and costly, since it can generate new solutions based on very few observations.
To give an example, imagine you’re trying to optimize the sequence of amino acids in a protein design for a new drug. Calculating the cost function here could be very expensive, since the drug would need to be synthesized and tested to evaluate it.
With GEO, it doesn’t matter how you calculate the cost function, nor will GEO replace your existing code or process for evaluating the cost function. GEO only needs the outputs of the cost function evaluation — the cost values — so it can learn which variables correspond to low-cost solutions and then propose new solution variables.
One of the biggest advantages of GEO is that it can only improve with time. This is due to the flexibility of using different generative models, traditional optimizers to train these models, and different hardware to run these models. As both generative models and traditional optimizers become more powerful, GEO will in turn become more powerful as well.
A bigger step change could occur as quantum hardware improves. Given the low power and high error rates of today’s quantum hardware, you’re better off using quantum algorithms that run on classical hardware. But as quantum devices become more powerful and error-correcting, the advantages of quantum generative models in generalization and expressivity will have a greater impact on GEO. What’s more, the quantum models running on classical hardware today can be easily adapted to run on quantum hardware in the future, setting up users for additional advantages.
As both generative models and traditional optimizers become more powerful, GEO will in turn become more powerful as well.
Imagine the landscape of possible solutions like a geographic landscape, with low-cost solutions represented by valleys and depressions and high-cost solutions being peaks. Many conventional optimization algorithms work by starting somewhere and then following the slope downhill, tweaking the variables slightly until they come to the local minimum.
But chances are, there is a lower local minimum — a deeper hole — somewhere else. The local optimizer won’t be able to find it unless it starts again from a different point. For some optimization problems, the landscape is particularly difficult to navigate — imagine a mountain range with many peaks and valleys isolated from each other. The local optimizer would struggle here.
Other optimizers do a global search, searching for multiple local minimum to find the lowest one. By learning the distribution of multiple local minimum generated by other algorithms, GEO has a better chance of finding the global minimum in the energy landscape.
Many local optimization algorithms only compare new solutions with the most recently generated solutions — everything else is forgotten. In contrast, GEO proposes solutions by leveraging the entire history of candidate solutions. In other words, the more data on existing solutions you have, the better results you can get with GEO. This makes GEO ideal for problems with many existing solutions that meet the constraints, but where a better target value is desired.
The more data on existing solutions you have, the better results you can get with GEO.
Manufacturing plant scheduling optimization and portfolio optimization are just the tip of the iceberg for what you can accomplish with GEO. As mentioned earlier, GEO is a universal solver that can be flexibly applied to any optimization problem.
More GEO use cases can be found on our industry-specific solution pages (hyperlinked by each industry below or found under “Solutions” in our website navigation menu). Below are some examples of potential use cases in each industry.
Network Planning Optimization
Save costs by more efficiently balancing concerns for demand, crew scheduling, fuel planning, and more when scheduling and routing fleet vehicles.
Chemical Reaction Optimization
Optimize chemical reaction network conditions to maximize yield, reduce costs, and save time.
Inventory Optimization
Prevent overflows and stock-outs by optimizing production cycles and shipments for raw materials or finished products.
Energy Production Site Optimization
Optimize the placement of solar panels, wind turbines, and other energy production sites to maximize output and minimize costs.
Portfolio Optimization
Optimize capital allocation among portfolio assets to maximize returns and reduce risk while respecting investment constraints.
Public Health Supply Chain Optimization
Balance multiple objectives, such as product quality, costs, delivery times, and demand coverage to reduce shortages and waste in the public health supply chain.
Protein Design
Improve protein functionality by optimizing the sequence of amino acid–rotamers in an active site without altering the backbone structure.
Supply Chain Optimization
Optimize the selection of suppliers, distributors, and vendors for product quality, costs, delivery times, and demand coverage.
Manufacturing Process Optimization
Optimize the design of factories, employee schedules, and machine processes to reduce waste.
Wireless Transceiver Location Optimization
Optimize the locations of new broadband and 5G access points to maximize return on investment network coverage.
