Zapata AI Speeds Up Monte Carlo Simulation +8,000x for the Financial Services Industry

Zapata AI Speeds Up Monte Carlo Simulation +8,000x for the Financial Services Industry

Given the enormous complexity of the financial services economy, Monte Carlo simulations typically have intense calculation workloads that can be extremely expensive from a computational perspective. These calculations only get more expensive the more asset classes, allocation scenarios, and related variables are introduced, representing a large fraction of financial institutions’ total compute costs.
Using mathematical concepts first developed for highly specialized calculations in quantum physics and quantum information science, Zapata AI has implemented an innovative alternative to Monte Carlo simulations that dramatically reduces the time required to run these crucial calculations, while reducing their costs as well. In some scenarios, we’ve demonstrated that our method can provide a speed up of over 8,000x the time it takes to run a comparable Monte Carlo simulation using traditional techniques on the same computational hardware.
Before we get into the details of this technique and its implications for the financial services industry, let’s start with some background on risk management and the importance of Monte Carlo simulations.
Risk management is a fundamental, core principle to ensuring the stability of the financial services industry. One of the clearest and most devastating examples of risk management gone awry was the 2008 financial crisis, where (to grossly oversimplify) excessive risks taken by global financial institutions culminated in a worldwide economic meltdown which threatened the existence of economies around the world.
Since the 2008 financial crisis, new regulations like the Basel III accords and CCAR have mandated stricter stress testing and risk management practices in finance.
Since the 2008 financial crisis, new regulations like the Basel III accords and the Comprehensive Capital Analysis and Review (CCAR) have been implemented to mandate stricter stress testing and risk management practices. These regulations are designed to ensure that banks and other financial institutions have access to sufficient capital and liquidity to mitigate bank runs in the event of another economic crisis.
However, meeting these regulations is easier said than done, considering the size and complexity of many financial services institutions and their portfolios as well as the vast scale, interconnectedness, and unpredictability of the global economy. To successfully manage risk and meet these regulations, financial institutions must carefully consider and account many commingled and contingent factors, from dynamic asset pricing and counter-party risk to macroeconomic market variables — to name a few.
As the number of these contingent risk factors grows, the computational resources required to calculate the risk with Monte Carlo methods grows dramatically.
To make such considerations effective, financial institutions rely on quantitative analyses of the aggregate statistical behaviors of vast combinations of these contingent factors. Such quantitative analyses are often formulated and expressed as mathematical operations in high-dimensional spaces. A typical paradigm for addressing the complexity of high-dimensional problems is by Monte Carlo sampling, also known as Monte Carlo simulation. These Monte Carlo methods are also commonly used to price financial derivatives, such as option contracts.
The technical details of addressing these high-dimensional problems with Monte Carlo methods are less important for the scope of this story. The crucial point is that as the number of these contingent risk factors grows, the computational resources required to calculate risk with Monte Carlo methods grows dramatically. With these risk analyses increasingly required for regulatory compliance, Monte Carlo-based quantitative risk analysis calculations have become an ongoing and significant inelastic cost for many financial services institutions.
Monte Carlo-based quantitative risk analysis calculations have become an ongoing and significant inelastic cost for many financial services institutions.
Monte Carlo methods are not limited to finance. They’re also widely used in computational science, especially in branches that seek to model complex natural phenomena such as quantum physics, quantum chemistry and fluid dynamics.
The Zapata AI team has extensive experience in these fields owing to our background in quantum computing. As such, we have been developing new, innovative computational techniques based on insights from quantum science that have proven far more performant than traditional Monte Carlo methods in many settings.
These quantum techniques have so far been primarily known and employed in highly specialized computational science problems plagued by the so-called “curse of dimensionality.” These are computational problems that are so high dimensional that even the largest and most powerful supercomputers in the world can not come close to solving them.
We have been developing new computational techniques based on insights from quantum science that have proven far more performant than traditional Monte Carlo methods in many settings.
Zapata has since been pioneering the application of these quantum techniques to everyday commercial and enterprise business problems — in particular in the financial services industry. Notably, our numerical benchmarking experiments have shown that our quantum techniques are many orders of magnitude faster than traditional Monte Carlo in converging on a solution when controlling for the same computational resources.
Consider a multi-asset option pricing problem, which typically requires Monte Carlo simulations in practice.
For a problem of 10 assets (left) and 20 assets (right), the figure below compares the convergence of the traditional Monte Carlo method and our Fast Alternative to Monte Carlo (FATMC), with both using the same CPU resources. With 10 assets, we observed an 8,400-fold speedup of FATMC over Monte Carlo, and an 1,800-fold speedup with 20 assets.
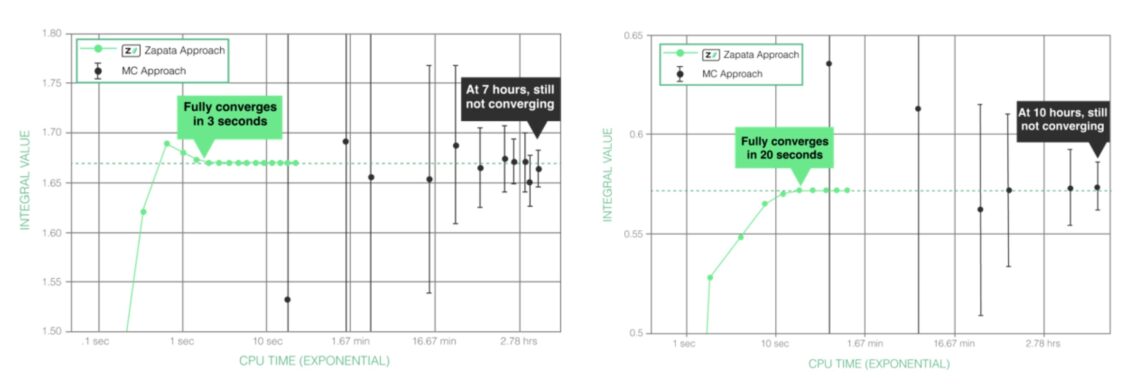
The value is clear: FATMC could dramatically reduce the time, resources and costs associated with running high-dimensional calculations in financial services use cases which typically require Monte Carlo simulations — without sacrificing accuracy.
Monte Carlo simulations are commonly used to assess the risk and return profiles of investment portfolios. By simulating a wide range of market scenarios, investors can understand how different asset allocations might perform under various market conditions. This helps in evaluating the probability of meeting investment goals and the potential for extreme losses (tail risk), aiding in effective portfolio diversification and risk management strategies. FATMC could help asset or portfolio managers understand how different asset allocations might perform under various market conditions much faster and at a significantly lower cost than if they were using a Monte Carlo simulation.
Monte Carlo methods are particularly useful in valuing options and other financial derivatives where the payoff is dependent on the future price path of the underlying asset. Monte Carlo simulations can model the stochastic behavior of asset prices over time, allowing for the pricing of complex derivatives and the assessment of their risk profiles. Here too, FATMC could help dramatically speed up option pricing and derivative valuation, modeling the stochastic long-term behavior of underlying asset prices more quickly and at a lower cost than traditional Monte Carlo simulations.
Value at Risk is a widely used risk management tool in finance that estimates the potential loss in value of a risky asset or portfolio over a set period under normal market conditions. Monte Carlo simulations can be used to calculate VaR by simulating thousands of possible price paths for the assets in a portfolio and then determining the potential losses. This approach is useful for capturing the risks in portfolios that contain complex, nonlinear instruments like options, as it does not rely on the normal distribution assumption and can model the fat tails and skewness often observed in financial returns. FATMC could also be used to calculate VaR faster or at a lower cost than traditional Monte Carlo simulations.


